<<< назад
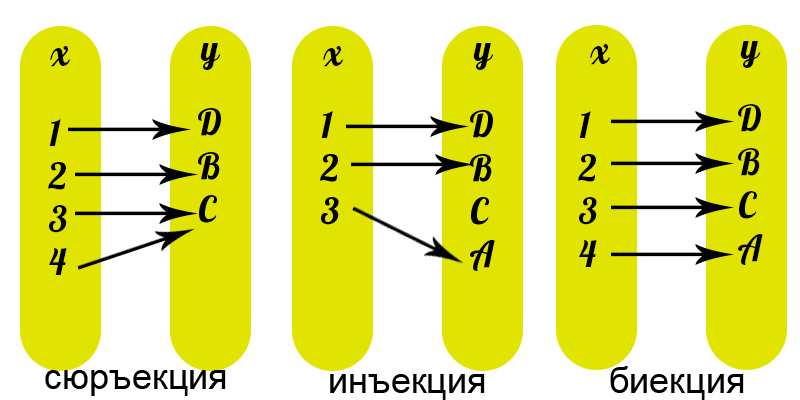
Сюръекция, инъекция и биекция.
- Отображение f:x->y называется СЮРЪЕКЦИЕЙ, если Ay∈Y ∃ x∈X:y=f(x). Тогда y - образ, x - прообраз y.
- Отображение f:x->y называется ИНЪЕКЦИЕЙ, если x1 ≠ x2 => f(x1)≠f(x2), те разные элементы множества X переводятся в разные элементы множества Y.
или f(x1)≠f(x2) => x1=x2
- Отображение f:x->y называется БИЕКЦИЕЙ, если оно одновременно сюръективно и инъективно. При биективном отражении каждому элементу одного множества соответсвует ровно один элемент другого множества, при этом определено обратное отображение, которое обладает теми же свойствами.